Air source heat pump heating design and construction guide
Second, the ideal refrigeration (heating) cycle - reverse Carnot cycle
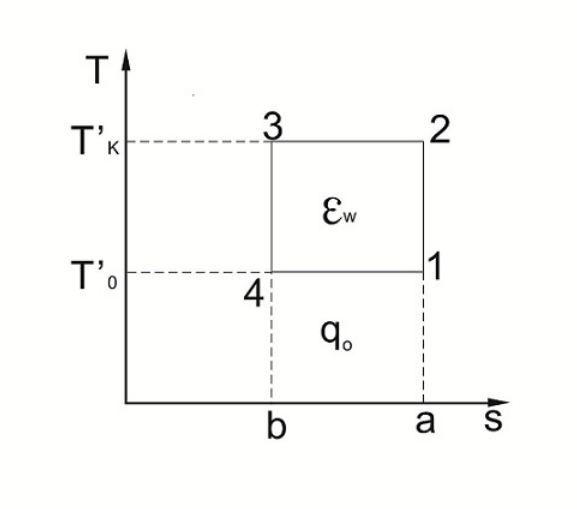
The Carnot cycle is divided into a positive Carnot cycle and an inverse Carnot cycle, both of which are composed of two isothermal processes and two adiabatic processes, which are a theoretical cycle. As shown in the figure, 1-2-3-4-1 is the inverse Carnot cycle. In the inverse Carnot cycle, the refrigerant expands along the adiabatic line 3-4, and the temperature is lowered from the heat source temperature T'k to the cold source temperature T' 0; then evaporating along the isotherm 4-1, the working fluid is again adiabically compressed from 1 to state 2, and finally condensed along the isotherms 2-3. The refrigeration coefficient can be derived, that is, the ratio of the cooling capacity to the input electric power: ε = Q / W
The refrigeration coefficient of the inverse Carnot cycle, independent of the refrigerant, depends only on the temperature of the cold heat source. The lower the temperature of the cold source (indoor), the higher the temperature of the heat source (outdoor), and the smaller the coefficient of refrigeration. At the same time, the influence of the cold source temperature is greater than the influence of the heat source temperature. This explains why our air conditioners, the hotter the summer days, the less force.
Reverse Carnot cycle heating coefficient
ε= T'k / (T'k -T'0 )
The heating coefficient of the same inverse Carnot cycle also depends only on the temperature of the cold heat source. When the temperature of the heat source (indoor) is constant, the temperature of the cold source (outdoor) decreases, the temperature difference between the indoor and outdoor (denominator) increases, and the heating coefficient (ie, heating capacity) decreases. This is what we said, the colder the winter, The heat pump does not give force. That is, "reverse effect."

